Coordenadas polares

Sistemas de coordenadas e bases

Na Geometria Analítica, aprendemos a usar sistemas de coordenadas retangulares para

criar uma correspondência bijetora entre os pontos do espaço bidimensional e os pares

ordenados de números reais, bem como entre os pontos do espaço tridimensional e os

ternos ordenados de números reais. Embora os sistemas de coordenadas retangulares sejam comuns, eles não são essenciais. Por exemplo, a figura a seguir mostra sistemas de coordenadas nos espaços bi e tridimensionais em que os eixos coordenados não são mutuamente perpendiculares:

Com o efeito, da Geometria elementar sabe-se que por um ponto dado fora de uma reta passam uma única paralela a essa reta. Assim, dados dois eixos (ou três no caso do espaço) concorrentes quaisquer, o processo já descrito na construção do sistema de coordenadas cartesianas (retangulares) pode ser utilizado para estabelecer uma correspondência biunívoca entre pontos do plano e pares ordenados de números reais.

Mudança de sistema de coordenadas

Vamos voltar ao nosso problema de descrever o movimento de uma partícula. Se ela se move em um plano, utilizamos de uma par ordenado de números reais para localiza-la no espaço em cada instante.

Como temos liberdade na escolha de onde fixarmos nosso sistema de coordenadas, isto é, podemos escolher qualquer ponto como a origem O do nosso sistema de coordenadas (vamos ver uma interpretação física na seção seguinte) poderíamos pensar em como simplificar a descrição da posição da partícula. O mais simples possível, seria se a origem coincidisse com a posição da partícula em todo instante, mas isso não é interessante uma vez que queremos descrever o movimento dela - se a posição r(t) = 0, para todo t, então v = a = 0 para todo t, e não teríamos nada. De fato, se queremos descrever o movimento da partícula, precisamos de um referencial externo (uma outra partícula). No entanto, em alguns problemas, mudar a origem do nosso sistema de coordenadas simplifica a descrição do problema, e isso é feito facilmente com uma translação do nosso sistema de coordenadas.

Obs: A ideia de mudar a origem do sistema de coordenadas é muita importante para diversos problemas na física principalmente quando falamos de um sistema de partículas, no qual a descrição tomando como referencial o centro de massa do sistema é bastante simplificada.

Translação de um sistema de coordenadas cartesianas

Suponha que uma partícula descreve um movimento circular de raio R no plano. A trajetória, isto é., o círculo de raio R centrado em r0, é definida como o conjunto de posições da partícula tal que a distância dela até o ponto r0 é sempre constante durante o movimento e portanto igual a R. A equação vetorial da trajetória é

Se utilizamos um sistema de coordenadas cartesianas, a equação acima é equivalente à

Façamos agora uma escolha de referencial mais apropriada. Notavelmente, por ser o ponto r0 fixo, a sua "existência" na equação da trajetória em nada acrescenta ao nosso conhecimento sobre o movimento da partícula: olhando o movimento de onde estamos fazendo ou a partir do ponto r0, sabemos que a partícula se move em um círculo.

Podemos fazer uma mudança de sistema de coordenadas de modo a simplificar a equação acima, descrevendo o movimento a partir a partir do centro r0. Isso é equivalente a tomar a origem de um novo sistema de coordenadas cartesianas O'x'y' coincidindo com r0, isto é, O' = r0 = (x0, y0). No sistema O'x'y', O' = (0, 0), assim a transformação do sistema Oxy para o O'x'y' é dado por

e temos as equações de mudança de sistema de coordenadas

de modo que a equação da trajetória no sistema O'x'y' é

A mudança na medida da posição da partícula não implica em mudanças na suas taxas de variação, uma vez que r0 é constante, ou seja, tanto a velocidade quanto a aceleração medidas com as novas coordenadas são as mesmas que quando medidas com as antigas pois

assim, essa transformação é uma simetria do nosso sistema; uma translação desse tipo não afeta em nada as equações do movimento bem como a física do problema.

Rotação de um sistema de coordenadas cartesianas

Discutimos anteriormente como poderíamos simplificar a descrição da posição de uma partícula. O segundo caso mais simples seria um sistema de coordenadas no qual a partícula estaria sobre um dos eixos. Fazemos isso efetuando uma rotação

Considere um ponto P com coordenadas (x1, x2, x3) em relação a um certo sistema de coordenadas cartesianas. A seguir, considere um sistema de coordenadas diferente, que pode ser gerado a partir do sistema original por meio de uma simples rotação. Considere as coordenadas do ponto P em relação ao novo sistema de coordenadas como sendo (x'1, x'2, x'3)

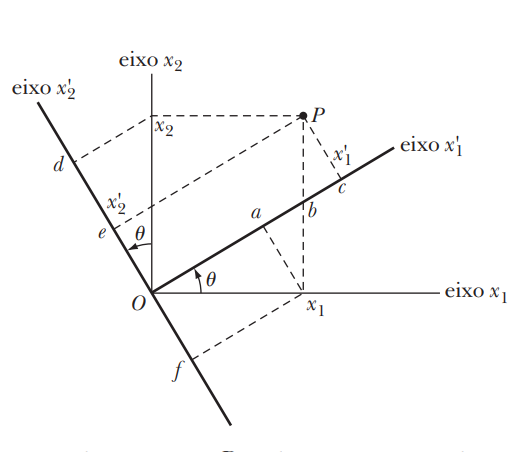
Da figura acima, tem-se

Vamos apresentar a notação a seguir: expressamos o ângulo entre o eixo x'1 e o eixo x1 como (x'1, x1) e, em geral, o ângulo entre o eixo x'i e o eixo xj é indicado por (x'i, xj).

Além disso, definimos um conjunto de números λ{ij} por

Portanto, para a figura acima, temos

As equações de transformação agora se tornam

Desse modo, em geral, para três dimensões temos

ou, em notação de somatória,

A quantidade λ{ij} é denominada cosseno diretor do eixo xi em relação ao eixo xj. É conveniente organizar λ{ij} em um arranjo quadrado denominado matriz.

λ é chamada de matriz de transformação ou matriz de rotação.

As coordenadas de um ponto podem ser expressas como uma matriz coluna

De modo que podemos representar a equação de mudança de coordenadas por um produto matricial.

Vamos discutir algumas propriedades da matriz de rotação λ. Antes precisamos de dois resultados.

O primeiro resultado de que precisamos é a identidade

Considere, como na figura abaixo, um segmento de linha se estendendo em certa direção no espaço. Escolhemos uma origem para o nosso sistema de coordenadas que se encontre em algum ponto da linha. A linha então forma alguns ângulos definidos com cada um dos eixos de coordenadas. Tomemos os ângulos formados com os eixos x1,x2, x3 como sendo α, β e γ. As quantidades cos (α), cos (β), cos (γ) são denominadas cossenos diretores da linha

Seja P = (x1, x2, x3) o ponto da outra extremidade do segmento com x1, x2 ≠ 0 e r o comprimento do segmento, ou seja, r = √ (x1² + x2²+ x3²). Da figura acima, tem-se

Além disso, aplicando a lei dos cossenos, tem-se

Portanto

Em segundo lugar, se temos duas linhas com cossenos diretores cos (α), cos (β), cos (γ) e cos (α'), cos (β'), cos (γ'), o cosseno do ângulo θ entre essas linhas é fornecido por

Seja P = (x1, x2, x3) o ponto da outra extremidade do segmento (α, β, γ) com x1, x2 ≠ 0 e r0 comprimento desse segmento, ou seja, r = √ (x1² + x2²+ x3²). Igualmente para o outro segmento (α', β', γ') com P = (x'1, x'2, x'3) e comprimento r'.

Pela lei dos cossenos:

Do que vimos anteriormente, temos

Expandindo os quadrados das diferenças e utilizando os resultados

tem-se

Donde segue

Com um conjunto de eixos x1, x2, x3, vamos agora efetuar uma rotação arbitrária sobre algum eixo através da origem. Na nova posição, rotulamos os eixos como x'1, x'2, x'3. A rotação

das coordenadas pode ser especificada fornecendo-se os cossenos de todos os ângulos entre os vários eixos, em outras palavras, por meio de λ{ij}.

Em primeiro lugar, o eixo x'1 pode ser considerado ele próprio como sendo uma linha

no sistema de coordenadas (x1, x2, x3). Os cossenos diretores dessa linha são (λ{11},λ{12},λ{13}). Similarmente, os cossenos diretores do eixo x2 no sistema (x1, x2, x3) são fornecidos por (λ{21},λ{22},λ{23}) . Pelo fato de o ângulo entre o eixo x'1 e x'2 ser π/2, aplicando a equação anterior, temos:

Podemos escrever isso na forma de somatório

Em geral

Pelo fato de a soma dos quadrados dos cossenos diretores de uma linha ser igual à unidade, temos para o eixo x'1 no sistema (x1, x2, x3),

Ou

e, em geral,

Podemos combinar os resultados fornecidos pelas equações acima como

A validade da equação acima depende das coordenadas dos eixos em cada um dos sistemas sendo mutuamente perpendiculares. Esses sistemas são ortogonais, e essa equação é a condição de ortogonalidade, onde δ{ik} é o símbolo delta de Kronecker, que é definido por

Notemos que o símbolo delta de Kronecker é o elemento da matriz identidade

Se considerássemos os eixos x como linhas no sistema de coordenadas x' e efetuássemos um cálculo análogo aos nossos cálculos precedentes, encontraríamos a relação

Alguns resultados interessantes surgem quando pensamos na rotação de um sistema de coordenadas em termos de matrizes. Um dos principais resultados é que matriz transposta λ^t da matriz de rotação λ é a sua inversa. Com efeito,

Com esse resultado, podemos obter a equação inversa para a mudança de sistema de coordenadas

Sistema de coordenadas polares

Toda discussão anterior se iniciou na busca de um sistema de coordenadas que facilita-se a descrição da posição de uma partícula. É claro que se não há restrição sobre o movimento da partícula, eventualmente sua posição não será sobre um dos eixos e então uma única rotação do sistema de coordenadas não terá ajudado. No entanto, se para cada ponto tomarmos um sistema de coordenadas rotacionado tal que esse ponto esteja sobre um dos eixos teremos de fato simplificado nosso problema. Fazer isso, é permitir que o ângulo θ, no caso de um sistema de coordenadas no plano, mude para cada ponto. Construímos então um novo sistema de coordenadas:

Fixado no plano um semieixo Ox (tal semieixo denomina-se eixo polar, e o ponto O, polo), (esse eixo é geralmente desenhado horizontalmente para a direita e corresponde ao eixo x positivo nas coordenadas cartesianas) cada ponto P do plano fica determinado por suas coordenadas polares (r, θ), em que θ é a medida em radianos do ângulo entre o segmento OP e o eixo polar (usamos a convenção de que um ângulo é positivo se for medido no sentido anti-horário a partir do eixo polar e negativo se for medido no sentido horário.) e r é a distância de O até P; assim r ≥ 0.

Se P = O, então r = 0, e convencionamos que (0, θ) representa o polo para qualquer valor de θ.

Uma desvantagem de utilizar coordenadas polares reside no fato de que a correspondência acima descrita não é biunívoca, já que se um ponto P do plano é dado em coordenadas polares por (t, θ), então todos os pares da forma (r, θ + 2kπ), com k ∈ Z, são associados a P. Além disso, as coordenadas polares da origem O não são bem definidas.

No entanto, para muitos problemas basta tomarmos r ∈ [0, ∞ ) e θ ∈ [0, 2π). Com isso, relacionamos as coordenadas polares com as retangulares pelas seguintes equações:

De modo que o vetor posição é dado por r = rcos(θ)x + rsin(θ)y.

Obs: Essas equações são válidas mesmo se θ ≥ π/2. Por exemplo, considere P pertencente ao segundo quadrante

Então, devemos tomar - x (pois x < 0) para o comprimento de um dos lados do triângulo retângulo. Além disso, α = π - θ, e portanto

Para um ângulo especifico θ sabemos que as equações de mudança de coordenadas (no plano) são

Substituindo x = rcos(θ) e y = rsin(θ) nas equações, tem-se

Assim, uma vez dada as coordenadas polares (r, θ) identificamos um sistema de coordenadas cartesianas Ox'y' obtido por uma rotação de um ângulo θ tal que as coordenadas do ponto sejam (r, 0). Como para cada ponto esse sistema muda, passamos a chamar x' = r e y'= θ. Nesse sistema um vetor é dado por

onde r é o vetor unitário do eixo r, ou seja é um vetor diretor do eixo r. Esse vetor unitário é relacionado com os vetores unitário x e y fixos, pela seguinte expressão

E o vetor unitário θ do eixo θ é dado por

de tal modo que r x θ = 0

Movimento em termos dos vetores r e θ

Na descrição do movimento de uma partícula no plano, as suas coordenadas de posição são parametrizadas no tempo, isso é, r e θ são funções do tempo. Podemos interpretar o sistemas de coordenadas Orθ como um sistema que acompanha o movimento da partícula. Assim, os vetores r e θ também variam com o tempo. Com isso, a velocidade v e a aceleração a são obtidos por

onde usamos a regra do produto para funções vetoriais.

Assim, a velocidade é

E a aceleração

usando a notação de ponto para a derivada afim de simplificar a escrita, tem-se